

Les listes simplement chaînées, dont j'ai parléau chapitre précédent sont très utiles, mais elles présentent néanmoins un inconvéniant majeur: on ne peut les parcourir que dans un sens… ce qui revient à peu près au même que si… vous n'aviez que la marche avant sur votre voiture.
En effet, elles fonctionnent très bien tant que, étant à l'élément N de la liste, vous souhaîtez accéder à l'élément N+X (ou X serait n'importe quel nombre positif)…
Les choses se corseront énormément, non pas du point de vue de la programmation en elle même, mais bien du point de vue du temps nécessaire pour atteindre l'élément recherché, si, étant à l'élément N de la liste, vous souhaîtez accéder à l'élément N-X (ou X serait n'importe quel nombre positif plus grand que N/2)…
Pour vous faire bien prendre conscience de ce que je tente de vous expliquer, imaginons un instant que nous disposions d'une liste composée de 10.000 éléments, et que nous soyions actuellement à l'élément 9700…
Si nous nous rendions compte, au fil de différents tests qu'il est maintenant nécessaire d'accéder à l'élément 9699, du fait que nous n'avons que la marche avant, nous serions partis pour rentrer dans une boucle qui, partant du premier élément de la liste accéderait… 9699 fois à l'élément suivant, ce qui prendrait fatalement un temps incroyable, alors que, si la marche arrière était présente, il suffirait d'accéder… une seule fois à l'élément précédent… ce qui serait 9699 fois plus rapide.
Mieux même, en étant au 9700ieme élément de la liste, faire marche arrière pour accéder à n'importe quel élément entre le 4851eme et le 9699eme s'avérerait plus rapide que le fait de repartir du début…
Et, bien évidemment, le raisonnement peut s'appliquer quel que soit l'élément sur lequel nous sommes à un moment donné.
Seulement, voilà, les listes simplement chaînées ne donnent pas cette possiblité d'accéder à l'élément qui précede celui sur lequel on se trouve…
C'est ici qu'entrent en jeu les listes doublement chaînées.
Finalement, le raisonnement que l'on suivra sera relativement simple: qu'il suffise que l'on mette une référence vers l'élément qui précède dans la structure que l'on crée, et nous pourrons parcourir la liste dans les deux sens.
La représentation de la liste en mémoire sera fort proche de ceci:
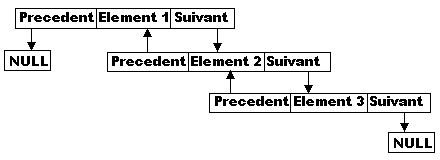
Les listes doublement chaînées ne peuvent malgré tout pas *forcément* être considérées comme la panacée dés que la décision d'avoir recours à une liste est prise.
Il faut en effet bien rester conscient du fait que, si cela nous permet d'accélerer l'acces à certains éléments de la liste, cela se fera malgré tout aux dépends de la mémoire qui est nécessaire pour gérer à chaque fois la référence à l'élément qui précede.
De plus, tout comme il n'est pas réellement intéressant de rouler à 140km/h sur autoroute plutôt qu'à 120 (la limite actuelle en Belgique), ou, du moins, sur courtes distances (le temps gagné est négligeable par rapport aux risques… pris pour le portefeuille principalement), si l'utilisation de la liste ne prévoit que de passer à l'élément suivant, une liste doublement chaînée revient bien souvent à sortir le canon pour tuer un moustique…
Il s'agira donc de prendre quelques instants pour décider s'il est préférable de gagner un peu de temps ou d'économiser un peu de mémoire…
En plus, elles ne seront réellement efficaces qu'à partir du moment où elles seront triées d'une manière qui correspond à l'idée "logique" que l'on se fait du tri dans le contexte de leur utilisation.
La structure qui nous intéressera sera en grande partie identique à celle que l'on utilise pour une liste simplement chainée.
Il suffira dans bien des cas de rajouter un pointeur vers l'élément qui précède.
Seulement, le fait de disposer d'un pointeur vers l'élément qui précède ne fera pas tout…
En effet, il ne servira à rien si l'on ne dispose pas d'un moyen qui permette, sans l'ombre d'un doute, de déterminer s'il faut partir "vers l'avant " ou s'il faut retourer "vers l'arrière "… voire, si on n'a pas purement et simplement intérêt à reprendre depuis sont début… On appelle un tel moyen un identifiant.
Evidemment, l'identifiant devra, d'une manière ou d'une autre, être intégré dans les structures utilisées pour la liste.
Mais, le fait d'envisager d'ajouter un élément à une structure fait qu'il faut, aussi, réfléchir à la gestion de cet identifiant.
Deux grandes manière d'envisager l'identifiant:
La première est de se dire qu'il "suffit" de rajouter le nouvel élément en fin de liste, et de lui donner comme valeur d'identifiant la valeur de l'identifiant de l'élément précédent +1.
La deuxième est de mettre au point un système qui assure une valeur unique, tout en étant suffisemment souple pour permettre que cette valeur ne soit pas dépendante des éléments qui précèdent et qu'elle n'influe en rien sur la valeur des éléments qui suivent.
Evidemment, ces deux optiques présentent des avantages et des inconvéniants (le contraire aurait été trop beau)…
La premiere a l'énorme avantage de ne pas nécessiter d'effort de conception particulier, mais présente l'inconvéniant de présenter une liste dont le tri ne correspond pas *forcément* à ce qui pourrait nous sembler un tri "logique" (par ordre de grandeur ou par ordre alphabétique, par exemple).
La deuxième optique a l'avantage de nous permettre de fournir une liste triée d'une manière "logique" (par ordre de grandeur ou par ordre alphabétique, par exemple), mais l'inconvéniant de nécessiter un effort de conception bien plus important.
Bien sûr, on pourrait envisager, si l'on en dispose, d'utiliser une valeur que l'on sait être unique -telle que le numéro de sécu ou un numéro de compte, par exemple- mais il faudrait alors être certain que le tri que cela implique sera ressenti comme "tri logique"… Mais ça, ce n'est que le contexte de l'application à créer qui pourra nous le dire  .
.
Reprenons l'exemple de l'appliction présentée au chapitre précédent.
Rajoutons y simplement le fait que l'on souhaite que la liste soit triée par ordre alphabétique, d'abord en fonction du nom, puis, au cas où deux personnes du meme nom devaient être mise dans la liste des contacts, en fonction de leur prénom.
NOTA:
*Idéalement*, il serait nécessiare de prévoir aussi le fait que deux personnes ayant le même nom et le même prénom puissent devoir être présente dans la liste et identifiée sans risque d'erreur… Mais cela ne ferait que compliquer inutilement l'exemple, qui tente malgré tout de rester simple
- Que doit faire l'application? L'application doit être en mesure de récupérer les informations concerant différents contacts et de les trier dés l'introduction
- De quelles informations l'application a-t-elle besoin? L'application a besoin du nom, du prénom et de l'adresse du contact
- Où l'application va-t-elle se procurer les informations? Toutes les informations seront introduites au clavier par l'utilisateur
- Comment l'application va-t-elle utiliser ces informations?
- L'application récupère le nom, le prénom et l'adresse du contact et calule un identifiant unique pour le contact
- L'application cherche dans la chaine la bonne place en fonction de l'identifant et insère le nouvel élément à sa place
- L'application renvoie une liste triées des différents contact
Les structures à utiliser dans cet exemples seront, finalement, fort proches des structures présentées dans les chapitres précédents.
Simplement, il s'agira de veiller à disposer, d'un identifiant et d'un pointeur vers l'élément précédent de la liste.
Si l'on part sur l'idée d'adapter les structures déjà vues, il ne fait que peu de doute que le pointeur vers l'élément précédent prendra place dans la structure Contacts, mais on peut se poser la question de savoir où aller placer l'identifiant…
Certaines personnes se baseront sur le fait que l'identifiant fait partie intégrante des coordonnées, au meme titre que le nom, le prénom (le numéro de sécu)… pour décider qu'il est logique de mettre l'identifiant dans la structure "Coordonnees "… Et elles n'auront pas tord.
D'autres pourront argumenter que l'identifiant et les coordonnées ne sont qu'une seule et même représentation de la personne, qu'il n'est pas logique qu'une chose soit, dans un même temps la chose et sa représentation, et que l'identifiant n'a un sens que dans le cas de la liste d'éléments à laquelle est rattachée la chose pour dire que l'identifiant sera bien mieux à sa place dans la structure Contacts… Et elles n'auront pas tord non plus…
Enfin, Le principe de "fainéantise" (qui cherche à tout de suite faire les choses le mieux possible dés le départ afin de ne pas devoir les recommencer par la suite, et donc, d'en faire le moins possible), appliqué par beaucoup de bons concepteurs, nous fait remarquer qu'il sera plus facile d'accéder à Element->identifiant qu'à Element->Data.identifiant
J'ai donc décidé de garder ma structure Coordonnee inchangée sous la forme de:
| Nom | type | Commentaire |
|---|---|---|
| Nom | 20 caractères | Pour garder le nom du contact |
| Prenom | 20 caractères | Pour garder le prénom du contact |
| Adresse | 50 caractères | Pour garder l'adresse du contact |
Et dont le code pour la créer ressemblera à s'y méprendre à:
structure Coordonnee
{
caracrere Nom[20] |
caractere Prenom[20] |
caractere Adresse[50] |
}
Et de modifier la structure Contact sous la forme de
| Nom | Type | Commentaire |
|---|---|---|
| Data | Coordonnee | permettra d'avoir le nom, le prénom et l'adresse de notre contact |
| id | entier | identifiant (unique) du contact (d'autres types auraient pu être envisagés ;) ) |
| Suivant | Contact | Pointeur qui contiendra l'adresse à laquelle trouver le contact introduit apres celui sur lequel on travaille |
| Precedent | Contact | Pointeur qui contiendra l'adresse à laquelle trouver le contact introduit avant celui sur lequel on travaille |
Le code pour la création de cette structure ressemblera à quelque chose du genre de:
Structure Contact
{
Coordonnee Data|
Entier Id|
Contact *Suivant |
Contact *Precedent|
}Comme l'identifiant prend ici une importance toute particulière, il est particulièrement important de réfléchir au meilleur moyen d'être sûr qu'il soit unique.
Je vous ai expliqué, quand j'ai présenté les types de bases habituellement utilisés, que la table de caractères ASCII comprenait 256 caractères et que n'importe quel caractère avait une valeur qui lui était propre comprise entre 0 et 255 …
Utilisons cette caractéristique pour au point un système de «pondération» de la valeur de chaque lettre en fonction de sa position dans le nom ou dans le prenom:

| Nom | Type | Commentaire |
|---|---|---|
| nom | 20 caractères | argument fournit contenant le nom du contact |
| prenom | 20 caractères | argument fournit contenant le prénom du contact |
| cpt | entier | variable servant de compteur |
| total | entier | total des valeurs pondérées des différents caractères (destiné à être renvoyé) |
Le code correspondant à cet algorithme, dans le langage que j'ai créé, sera:
Entier CreeId(nom, prenom)
{
cpt= 0|
total= 0|
nom = majuscule(nom)|
prenom = majuscule(prenom)|
{
total = total + nom[i]*255*(40-i)|
// nota, on aurait pu écrire total + (nom[i] * 255*(40-i)) mais
// l'ordre des priorités des opérations rend les parenthèses inutiles ;)
cpt = cpt+1 |
} Jusque (nom[i] = '\0' ou cpt > 20)
cpt =0 |
{
total = total+ prenom[i]*255*(20-i) |
cpt= cpt + 1 |
}Jusque(nom[i] = '\0' ou cpt > 20)
Renvoie total|
}
Pour éviter d'éventuels problèmes du fait de la casse des caractères (DZ apparaissant dans la liste avant Da), on transforme le nom et le prénom en majuscule.
Nous avons décidé, tout à fait arbitrairement, que le nom et le prénom étaient tous les deux représentés par des chaines de 20 caractères utiles.
Cela signifie que, si l'on venait à considérer une chaine NomPrénom qui serait la concaténation du nom et du prénom, nous arriverions à une chaine de 40 caractères utiles au total.
Le fait de multiplier la valeur du caractère par 255 (nombre de caractères possible) et par sa position permet de s'assurer que chaque caractère aura une valeur qui lui est propre en fonction de sa position et qu'il n'y a pas de risque d'obtenir une valeur identique par un autre moyen.
Seulement, si l'on travaille comme cela, le premier caractère a une valeur plus petite que le deuxième qui a lui-même une valeur plus petie que le troisième etc.
Or, quand on veut un tri par ordre alphabétique, la première lettre est celle qui a le plus d'importance, juste avant la deuxième, qui a elle-même plus d'importance que la troisième etc.
Le fait de multiplier par 40 (nombre de caractères utiles d'une chaine NomPrenom éventuelle) moins la position du caractère au sein de la chaine NomPrenom rétablit l'équilibre.
Les boucles doivent s'exécuter jusqu'à ce que le caractere "nul" soit rencontré (représentation classique de la fin de chaine) ou jusqu'à ce que l'on ai parcouru les 20 caractères utiles de la chaine, car il est toujours mauvais d'essayer de parcourir plus d'éléments qu'il n'y en a 
Evidemment, à chaque fois que l'on calcule la pondération d'un caractère, on rajoute cette valeur à un total "général".
Une fois que le nom et le prénom ont été parcourus, il n'y a plus qu'à renvoyer la valeur du total.
Un autre avantage non négligeable de ce genre d'algorithme de création d'un identifiant est qu'il permettra de créer facilement une recherche sur un nom partiel…
En effet, si l'on a inséré les noms de Dubois, Dunski, Dupon et Durant, ces quatre noms auront une valeur comprise entre ( 68*40*255+85*39*255) 1 538 925 et 1 548 870 (début des valeurs des noms commencant par DV), et il devient donc facile de faire exécuter une boucle qui cherche entre ces deux valeurs…
Lorsque l'on voudra effectuer une recherche, plusieurs possiblités s'offriront à nous:
Pour prendre ces deux cas en considération, deux grands courents de pensée vont, encore une fois, s'affronter.
Le premier sera d'estimer, très justement, qu'il vaut mieux limiter les routines à un but bien précis, et que l'on aurait donc intérêt à créer une routine pour la recherche de l'emplacement d'insertion et une autre pour récupérer un élément précis dans la liste.
Le deuxième s'inspirera de la fainéantise latente du concepteur qui nous fera remarquer, à titre tout aussi juste, qu'il n'y a qu'un parametre qui change entre les deux recherches, que la recherche en elle même suivra la même logique, pour estimer qu'il ne sert donc à rien de faire "deux fois le travail" en créant deux routines différentes (car cela signifie devoir écrire deux routines différentes, avec un code sensiblement identique).
Ces deux courents de pensée -bien qu'antagonistes- sont aussi valable l'un que l'autre, et il est fort probable qu'un même programmeur -selon son humeur,les impératifs apparus lors de la phase de réflexion, son état de fatigue ou, simplement selon le temps qui fait- décide dans certaines occasions de travailler en suivant l'un plutôt que l'autre, mais dans d'autres occasions de suivre "l'autre"…
Comme je suis soumis à une contrainte supplémentaire de taille pour que mon site reste correctement présenté, et pour vous laisser la possiblité de l'imprimer, je vous présente ici un algorithme qui choisi de créer deux fonctions (CherchePrecis et ChercheIntro)…
Cependant, il est fort vraissemblable que, si je devais créer un algorithme pour une utilisation plus "réelle" que ce site, j'aurais préféré la création d'une seule fonction, qui aurait, vraissemblablement, utilisé la récursivité.
Ceux qui seraient intéressés par l'algorithme que j'aurais vraissemblablement utilisé le trouveront, avec les explications, mais sans la mise en forme propre au site, sur cette page.

Le nombre et le type des arguments des deux fonction sont identiques, ainsi, d'ailleurs, que le type que chacune des fonctions renvoie.
Elles renverront toutes les deux un pointeur de type Contact correspondant à l'élément de la liste qui a été trouvé et prendront toutes deux un argument sous la forme d'un pointeur de type contact (nommé travail) comme "point d'acces" à la liste ainsi qu'un entier permettant d'avoir un identifiant de référence (nommé id).
La première chose que font ces deux fonctions est de vérifier si le pointeur fourni en argument est valide…
En effet, si l'on devait essayer d'accéder à l'élément Precedent ou Suivant d'un pointeur invalide, cela aurait des conséquences catastrophiques…
C'est la raison pour laquelle, si le pointeur de travail est nul, on le renvoie d'office pour sortir de la fonction (il s'agira, par la suite, de vérifier si le pointeur renvoyé par ces fonctions n'est pas nul, mais on en parlera plus tard).
A partir de là, les fonctions commencent à réagir différemment…
La fonction CherchePrecis() qui cherche un élément dont on a déterminé l'identifiant, afin d'accéder aux données qu'il contient va vérifier si l'identifiant du pointeur de travail est plus grand que l'identifiant fourni en référence afin de savoir s'il faut parcourrir la liste "vers l'avant" ou "vers l'arrière".
En fonction du test, on entrera alors dans une boucle qui cherchera l'élément Precedent ou l'élément Suivant, selon le cas, et dont on sort dans deux cas:
En tout état de cause, on renvoie le pointeur de travail trouvé lors du parcours de la liste (qui vaudra, là aussi, NULL si l'élément n'a pas été trouvé).
D'un autre coté, la fonction ChercheInsere(), qui, comme le nom vous l'indique peut être, cherche l'élément qui servira de référence pour l'insertion d'un nouvel élément dans la liste, doit aussi déterminer dans quel sens parcourrir la liste.
Du fait de mes contraintes de place, j'ai dû m'orienter vers des tests séparés, mais, il va sans dire que l'on aurait très bien pu envisager d'imbriquer le test Si travail->id > id dans la partie "non" du test Si travail = NULL et estimer que, si travail->id n'est pas plus grand que id, c'est en toute logique qu'il est plus petit, et donc, mettre la deuxième boucle dans la partie "non" du deuxième test …
Mais bon, les contraintes étant là… Autant donner les explications de l'algorithme que je vous soumet 
Donc, après s'être assuré que le pointeur de travail soit valide, nous vérifions si l'identifiant du pointeur de travail est plus grand que l'identifiant fourni comme référence.
Si c'est le cas, nous entrons dans une boucle qui parcoure la liste "vers l'arrière" afin de chercher un élément de la liste qui dont l'identifiant est plus petit que celui qui nous sert de référence, en veillant, en tout état de cause, à nous arreter au premier élément de la liste, même si l'identifiant de celui-ci est plus grand que notre référence (cela signifiera que l'élément que l'on s'apprete à rajouter prendra la première place dans la liste).
Une fois que l'on a déterminé l'élément, on le renvoie pour sortir de la fonction.
On n'atteindra donc la deuxième boucle que si… l'identifiant de notre pointeur de travail n'est pas plus grand que notre identifiant de référence.
Comme on a estimé, lors du calcul des identifiants, que l'on ne courrait pas énormément de risque d'avoir deux Jean Dupont différents, on peut estimer que, si l'identifiant de notre pointeur de travail n'est pas plus grand que notre référence c'est… qu'il est plus … Et qu'il faudra donc parcourir la liste vers l'avant.
La deuxième boucle réagira donc exactement comme la première, à ceci près qu'elle parcourera la liste vers l'avant, et s'arretera en tout état de cause au dernier élément de la liste, ce qui signifiera que l'élément que l'on s'apprete à rajouter prendra … la dernière position de la liste.
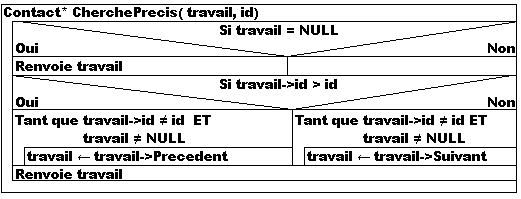
Le pseudo code pour ces deux fonctions sera:
Contact* CherchePrecis(travail, id)
{
Si (travail ==NULL)
{
Renvoie travail|
}
Si (travail->id >id)
{
TantQue(travail->id != id ET travai != NULL)
{
travail = travail->Precedent |
}
}
sinon
{
TantQue(travail->id != id ET travail !=NULL)
{
travail= travail->Suivant |
}
}
Renvoie travail |
}
Contact* ChercheInsere(travail, id)
{
SI(travail == NULL)
{
Renvoie travail |
}
SI(travail->id > id)
{
TantQue(travail->id > id ET
travail->Precedent != NULL)
{
travail = travail->Precedent |
}
Renvoie travail |
}
TantQue(travail->id < id ET
travail->Suivant != NULL)
{
travail = travail->Suivant |
}
Renvoie travail |
}N'oublions pas qu'il sera nécessaire de vider la liste une fois que nous n'en aurons plus besoin…
Encrore une fois, la récursivité peut venir à notre secours:

La fonction prendra un pointeur (nommé travail) de type Contact, et s'assurera que tous les éléments de la liste seront effacés.
Son mode de fonctionnement sera assez original: Pour chaque pointeur de travail, elle vérifiera s'il y a un élément précédent.
S'il y en a un, elle "séparera" l'élément précédent de la liste avant d'appeler la récursivité sur l'élément précédent.
Elle agira ensuite de la même manière face à l'élément suivant.
Enfin, elle libérera le pointeur de travail.
Il sera, dans la grosse majorité des cas, intéressant de créer un élément de la liste avant de l'insérer dans la liste.
Le plus simple consiste en une fonction qui prenne les informations du contact en parametre, et qui s'occupe uniquement de la création du noeud de la liste.

| Nom | Type | Commentaire |
|---|---|---|
| nom | 20 caractères | argument fournit contenant le nom du contact |
| prenom | 20 caractères | argument fournit contenant le prénom du contact |
| adresse | 50 caractères | Argument fournit contenant l'adresse du contact |
| Travail | Contact* | Pointeur de travail de type Contact |
Contact* CreeContact(nom, prenom, adresse)
{
Alloue Travail |
Si (Travail !=NULL)
{
Travail->Data->Nom = nom |
Travail->Data->Prenom = Prenom |
Travail->Data->Adresse = Adresse |
Travail->id = CreeId(nom, prenom) |
Travail->Precedent = NULL |
Travail->Suivant = NULL |
}
Renvoie Travail |
}
L'algorithme ne devrait pas poser énormément de problèmes:
Après avoir alloué dynamiquement un pointeur de type Contact, on teste si l'allocation a réussi, et, si c'est le cas, on fournit les valeurs adéquates, avant de le renvoyer à le fonction appelante.
Nota: A ce stade, le contact n'est pas encore inséré dans la liste, c'est la raison pour laquelle on définit les pointeur Precedent et Suivant à NULL.
J'ai, dans ce cas, choisi de faire comme si l'on avait déjà récupéré les valeurs intéressantes (nom, prenom et adresse), mais leur saisie par l'utilisateur pourrait très bien être effectuée au sein même de cette fonction… Ce n'est, encore une fois, qu'une question de "bon vouloir".
Comme la fonction CreeId() renvoie un entier, on peut très facilement l'utiliser pour déterminer la valeur de l'identifiant du contact que l'on vient de créer
Disposer d'une liste sans pouvoir y insérer un élément n'aurait que peu de sens.
Il est cependant indispensable de veiller à ne pas perdre un ou plusieurs éléments de la liste lors de l'insertion d'un nouvel élément, et donc, de mettre au point une logique stricte qui nous permette d'éviter cet écueil.
Le schéma de principe de l'insertion d'un élément dans la liste est le suivant:


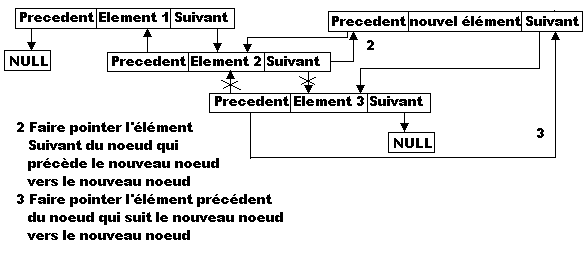
nota: S'il devait advenir que le nouvel élément doive prendre place avant le premier ou avant le dernier élément de la liste, la seule différence notable par rapport à ce schéma de principe est que, selon le cas, le pointeur Precedent ou le pointeur Suivant de l'élément rajouté pointerait sur… NULL, signifiant ainsi que l'élément rajouté devient le premier ou le dernier élment de la liste.
L'insertion d'un nouveau contact peut être considérée comme le fait de:
Evidemment, la fonction devra de toutes manières disposer d'un "point d'acces à la liste", qui devra être passé en paramètre.
L'algorithme correspondant serait représenté sous la forme de:

| Nom | Type | Commentaire |
|---|---|---|
| Entree | Contact* | Pointeur de type Contact fournit en argument contenant le "point d'entrée" de la liste |
| Travail | Contact* | Pointeur de type Contact à rajouter à la liste |
| nom | 20 caractères | Variable temporaire permettant l'introduction du nom du contact |
| prenom | 20 caractères | Variable temporaire permettant l'introduction du prenom du contact |
| adresse | 50 caractères | Variable temporaire permettant l'introduction de l'adresse ducontact |
Contact* Insere(Entree)
{
Affiche "Introdusez le nom " |
Acquiere nom |
Affiche "Introduisez le prenom " |
Acquiere prenom |
Affiche "Introduisez l'adresse " |
Acquiere adresse |
Travail = CreeContact(nom, prenom, adresse) |
Si (Travail != NULL)
{
Entree = ChercheInsere(Entree, Travail->id) |
Si (Entree = NULL)
{
Renvoie Travail |
}
Si (Entree->id > Travail->id)
{
Travail->Suivant = Entree |
Travail->Precedent = Entree->Precedent |
Travail->Precedent->Suivant = Travail |
Entree->Precedent = Travail |
Renvoie Travail |
}
Travail->Precedent = Entree |
Travail->Suivant = Entree->Suivant |
Entree->Suivant = Travail |
Travail->Suivant->Precedent = Travail |
}
Renvoie Travail |
}
Bon, à voir vos têtes, il semblerait que quelques explications soient les bienvenues…
Commençons donc par le commencement:
Pour pouvoir créer un noeud, il nous faut le nom, le prénom et l'adresse du nouveau contact. Il semble donc logique que l'on commence par demander à l'utilisateur de les introduire, en affichant un petit message lui indiquant ce qu'on attend de lui.
Nous aurions très bien pu, et ce serait d'ailleurs conseillé, décider d'utiliser la fonction d'acquisition sécurisée que je vous ai présentée à la page traitant des routines, et le code aurait alors été du genre de
Affiche "Introduisez le nom " | nom = Acquis(20) | Affiche "Introduisez le prenom " | prenom = Acquis(20) | Affiche "Introduisez l'adresse " | adresse = Acquis(50) |
Une fois que nous avons les valeurs il nous est possible de tenter la création d'un élément de la liste, c'est la raison pour laquelle nous indiquons que notre pointeur de travail reçoit la valeur renvoyée par la fonction CreeContact.
Evidemment, il faut s'assurer que la création du nouvel élément aie réussi, et c'est la raison pour laquelle presque tout le reste (à part le dernier renvoi) est mise dans la partie Vrai du test Si travail != NULL.
Il s'agit, une fois que l'on est sur que Travail existe, de récupérer… La place à laquelle il s'agira d'introduire notre nouvel élément dans la liste, et c'est pourquoi nous donnons à notre pointeur Entree (qui est notre point d'acces à la liste) la valeur renvoyée par la fonction ChercheInsere, dont le deuxième paramètre (l'identifiant qu'on prévoit d'ajouter) n'est autre… que l'identifiant de l'élément que l'on vient de créer.
Si on avait décidé d'utiliser la fonction récursive dont je vous ai parlé plus haut, le code pour l'appeler aurait été du genre de
Entree= Cherche(Entree, Travail->id, VRAI) |
Nous devons alors prendre trois possiblités en compte:
Les deux derniers cas à envisager viennent du fait que l'on ne sait a priori pas dans quel sens la liste a été parcourrue pour trouver notre élément de référence dans la liste.
Si la liste est vide, c'est relativement simple, l'élément que l'on vient de créer devient la liste… C'est la raison pour laquelle le premier test renvoie le pointeur de travail sans rien faire.
Dans les deux autres cas, il est primordial de veiller à ne pas perdre l'une ou l'autre partie de la liste…
C'est la raison pour laquelle on commence par lier notre pointeur de travail à l'élément qui doit le précéder dans la liste et à l'élément qui doit le suivre dans la liste.
Le schéma de principe à suivre est donné plus haut…
En tout état de cause, on renverra la valeur du pointeur de travail.
Ce renvoi aura la double utilité de servir d'élément courent de la liste et de permettre de vérifier si l'insertion s'est correctement déroulée (car il vaudra NULL si un problème d'allocation de mémoire pour le nouvel élément est apparu).
La vie est ainsi faite qu'il n'est pas possible d'être sûr à 100% que l'on restera "ad-vitam" en contact avec les gens…
Il est donc sensé de croire qu'à un moment ou un autre, on perde le contact avec quelqu'un, et que l'on estime devoir le supprimer de la liste.
Ici encore, il est absolument indispensable de veiller à travailler selon une logique stricte, afin de s'assurer que l'effacement d'un contact ne provoque pas l'effacement -ou, pire, la perte- de ceux qui le précèdent ou qui le le suivent dans la liste…
Pour y arriver, il faut, avant toute chose s'assurer que l'élément qui précède celui que l'on veut retirer soit en relation avec celui qui suit celui qu'on veut retirer.
Le schema de principe vous est donnés par les images qui suivent:
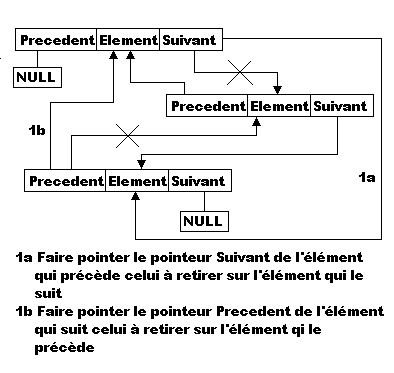
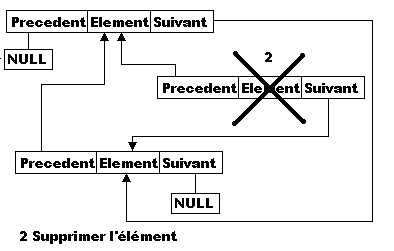
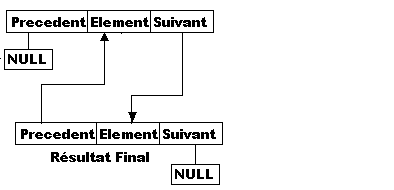
Plusieurs optiques sont valables, mais on peut considérer que, tout comme la fonction d'insertion peut s'occuper elle-même de la récupération des données, celle qui s'occupera de la suppression d'un élément peut se charger elle-même de récupérer les données qui lui permettront de sélectionner l'élément à supprimer.
Voici la logique à suivre:
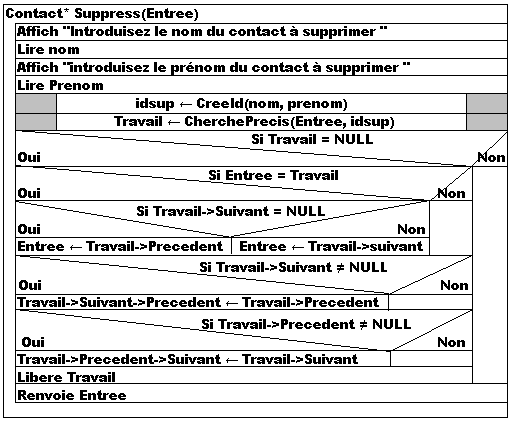
| Nom | Type | Commentaire |
|---|---|---|
| Entree | Contact* | Pointeur de type Contact fournit en argument contenant le "point d'entrée" de la liste |
| Travail | Contact* | Pointeur de type Contact à supprimer de la liste |
| nom | 20 caractères | Variable temporaire permettant l'introduction du nom du contact à supprimer |
| prenom | 20 caractères | Variable temporaire permettant l'introduction du prenom du contact à supprimer |
| idsup | Entier | Variable temporaire récupérant l'identifiant du contact à supprimer |
Contact* Suppress(Entree)
{
Affiche "Introduisez le nom du contact à supprimer " |
Lire nom |
Affiche "Introduisez le prénom du contact à supprimer " |
Lire prenom |
idsup = CreeId(nom, prenom) |
Travail = CherchePrecis(Entree, idsup) |
Si (Travail != NULL)
{
Si (Entree == Travai)
{
Si (Travail->Suivant = NULL)
{
Entree = Travail->Precedent |
}
Sinon
{
Entree = Travail->Suivant |
}
}
Si (Travail->Precedent != NULL)
Travail->Precedent->Suivant = Travail->Suivant |
Si (Travail->Suivant != NULL)
Travail->Suivant->Precedent = Travail->Precedent |
Libere Travail |
}
Renvoie Entree |
}
Une fois que l'on a déterminé l'identifiant de l'élément à supprimer, et que l'on a cherché cet élément dans la liste, il faut, avant tout, vérifier si l'élément existe.
Pour rappel, le fait d'essayer de libérer quelque chose qui n'existe pas risque de provoquer des catastrophes ![]() .
.
Dans le domaine des bases de données, on a coutume de dire que si plusieurs actions doivent modifier des valeurs, et que la base de données est cohérente avant d'effectuer ces actions, la base de données doit encore être cohérente une fois que toutes les modification ont été effectuées.
Le même principe doit être suivi ici:
Si, avant de supprimer un élément de la liste, vous disposez d'un point d'entrée valide pour accéder à la liste, il faut que vous disposiez, apres avoir supprimé l'élément, d'un point d'entré valide pour accéder à la liste.
Le principal problème auquel on peut être confronté, c'est que l'on peut vouloir supprimer l'élément qui nous sert justement de point d'entrée, qu'on ne le sait pas a priori, et que l'on ne sait pas, a priori, si cet élément n'est pas en début ou en fin de liste.
Avouez que cela fait beaucoup de choses qu'on ignore a priori… 
C'est la raison des tests imbriqués Si Entree = Travail et Si Travail->Suivant = NULL.
En effet, si Entree et Travail sont identiques, une fois que Travail aura été supprimé, notre point d'entrée pointera sur… quelque chose qui n'existe plus…
Il faut donc vérifier si on peut prendre L'élément précédent, ou s'il est préférable de prendre l'élément suivant.
J'en entends déjà certains se dire "oui, mais, si Travail->Suivant est nul et que Travail->précédent l'est aussi, Entree pointera vers une valeur nulle, et on sera tout aussi embêté"…
Hé bien non… Ce cas n'arrivera que si on supprime le seul élément de la liste (qui est, par défaut, le premier et le dernier)… et on se retrouvera donc avec un pointeur sur… une liste vide. Ce qui reste malgré tout cohérent dans cet unique cas bien précis.
Essayer de faire pointer le pointeur Predecent ou le pointeur Suivant d'un élément qui n'existerait pas vers quelque chose serait courrir droit dans un mur.
C'est la raison pour laquelle il est primoridal de s'assurer qu'ils existent bel et bien avant d'essayer de modifier une valeur qui s'y rapporte.
Nota: Des syntaxes du genre de Travail->Precedent->Suivant = Travail->Suivant ou Travail->Suivant->Precedent = Travail->Precedent sont sans doute de nature à en surprendre plus d'un…
Et Pourtant, elles sont malgré tout tout à fait correctes: Souvenez-vous…
Je vous indiquais dans le chapitre consacré à la pile qu'il est parfaitement possible, pour autant que l'on soit sûr de l'existance d'un élément, d'accéder au Nième élément avec un code du genre de
trouve=Dernier->precedent->precedent->precedentLe principe est ici exactement le même…
Si je prend, avec un élément de la liste nommé Actuel, le code Actuel->Suivant je suis bel et bien sur… L'élément qui suit Actuel dans la liste…
Cela reviendrait exactement au même que si j'avais un pointeur temporaire de type Contact et que je faisais Tempo = Actuel->Suivant
Comme je peux décider de redéfinir le pointeur Precedent d'un pointeur temporaire sous la forme de Tempo->Precedent = (une valeur), je peux donc décider de redéfinir le pointeur Precedent pour l'élément qui suit l'élément sur lequel je travaille sous la forme de Actuel->Suivant->Precedent = (une valeur) à condition, toujours, que je me sois assuré de l'existance d'un élément apres mon pointeur de travail Actuel…
Le code que je vous fournis revient donc exactement au même que, si, ayant un pointeur temporaire Tempo, j'avais écrit un code du genre de
Si (Travail->Precedent != NULL) { Tempo=Travail->Precedent| Tempo->Suivant = Travail->Suivant | } si (Travail->Suivant != NULL) { Tempo=Travail->Suivant| Tempo->Precedent = Travail->Precedent | }Accessoirement, le code suivant fonctionerait tout aussi bien…
Si (Travail->Precedent != NULL) { Tempo=Travail->Precedent| Tempo->Suivant = Tempo->Suivant->Suivant| } si (Travail->Suivant != NULL) { Tempo=Travail->Suivant| Tempo->Precedent = Tempo->Precedent->Precedent | }Quand je vous dis qu'il n'y a pas de mauvaise manière de faire (et je suis sûr qu'il y a encore d'autres manières d'y arriver… Vous n'aurez qu'à les chercher)
Copyright (©) 2005 (Philippe Dunski)
Ce cours est libre, vous pouvez le redistribuer et/ou le modifier selon les termes de la Licence Publique Générale GNU publiée par la Free Software Foundation (version 2 ou bien toute autre version ultérieure choisie par vous).
Ce cours est distribué car potentiellement utile, mais SANS AUCUNE GARANTIE, ni explicite ni implicite, y compris les garanties de commercialisation ou d'adaptation dans un but spécifique. Reportez-vous à la Licence Publique Générale GNU pour plus de détails.
Cependant, l'auteur apprécierait grandement que vous lui fassiez part de toute modification apportée à son contnu
Vous pouvez le contacter par mail à l'adresse koala01@free.fr
Vous pouvez trouver une adaptation française de la licence GNU/GPL à l'URL http://www.linux-france.org/article/these/gpl.html